噪声介绍
在现实中我们经常会遇到一些神奇的纹路,你说他们没有规律把,他们又有规律,你说他们有规律把,他们又不按照规律长。为了模拟出来这种效果,一堆大佬便发明出了噪音(Noise),ps:我还是不知道为什么叫做噪音而不是叫做其他的。由于噪声的强大,它被广泛用于程序生成,特效制作等各个方面,且使用方法多种多样
噪音从本质上看就是一些随机值,对于没有任何联系,完全随机的噪声图,我们称之为白噪声。而对于那些有规律的,有渐变的噪声图才是我们今天讨论的主角。
ValueNoise
因为ValueNoise最简单,因此我们第一个讲。ValueNoise图并不是完全随机出来的一张图。而是通过我们对关键点赋值,其他部分插值所得到的结果得到一张图,那么就意味着我们需要输入这些关键点的值。ValueNoise证正是一种基于晶格来生成的噪声图,那么什么是晶格呢?我们可以想想一个棋盘,里面的每一个格子便是一个晶格(没有找到好点的图片,将就用用把)
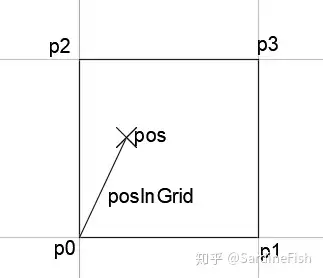
上面的一个方格便是一个晶格,ValueNoise的定义为我们需要输入每个晶格上四个顶点值,然后对于晶格内我们就可以利用插值来计算。对于晶格点的值的输入可以用Random来给一个随机值(最好别这么用。因为对于同一个点两个取值不一样会看起来比较奇怪),在这里我们给出的其他方法则是利用一个hash库。它可以保证我们只要输入的值相同那么输出肯定也相同。然后对于中间的点,我们可以用插值来计算,首先在P0和P1之间插值,P2和P3之间插值,再把他们两个的结果来根据Y值插值即可。代码如下
//保留整数,向下保留
float2 pi = floor(p);
//保留小数
float2 pf = frac(p);
//过度值
float2 w = pf * pf * pf*(6 * pf * pf - 15 * pf +10);
float v1 = lerp(hash21(pi+float2(0.0,0.0)),hash21(pi+float2(1.0,0.0)),w.x);
float v2 = lerp(hash21(pi+float2(0.0,1.0)),hash21(pi+float2(1.0,1.0)),w.x);
return lerp(v1,v2,w.y);
其中的W则是我们对插值的修饰,因为如果直接用坐标来作为值的话会显得十分的突兀,因此噪声的发明者提出了这个函数来修饰一下插值时的过度。完整代码如下
#pragma kernel CSMain
RWTexture2D<float4> Result;
float scale;
int Type = 0;
int state =0;
int size;
float2 hash21(float2 p){
float h = dot(p,float2(127.1,311.7));
return -1.0 + 2.0 * frac(sin(h) * 43758.5453123);
}
float ValueNoise(float2 p)
{
//保留整数,向下保留
float2 pi = floor(p);
//保留小数
float2 pf = frac(p);
//过度值
float2 w = pf * pf * pf*(6 * pf * pf - 15 * pf +10);
float v1 = lerp(hash21(pi+float2(0.0,0.0)),hash21(pi+float2(1.0,0.0)),w.x);
float v2 = lerp(hash21(pi+float2(0.0,1.0)),hash21(pi+float2(1.0,1.0)),w.x);
return lerp(v1,v2,w.y);
}
[numthreads(8,8,1)]
void CSMain (uint3 id : SV_DispatchThreadID)
{
float r =0;
r = ValueNoise(id/5);
r = r*0.5+0.5f;
Result[id.xy] = float4(r,r,r,1);
}
代码中 **r = ValueNoise(id/5)**中除以了5是为了确保一个晶格的长度为5,因为在脚本中我们是以分辨率为长度,而不是UV那样(0,1)为长度。所以不会出现小数,所以我们需要自己手动来处理一个缩放。如果这里不除以5,那么整个贴图就会变成一个白噪音图。
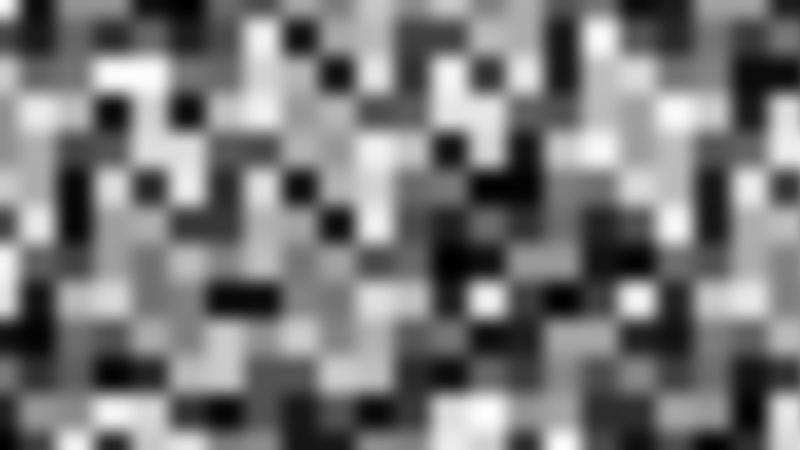
PerlinNoise
由于ValueNoise的插值不太人性,因此衍生出来了他的升级版PerlinNoise,
他与ValueNoise不同的点在于他给晶格上面的每一个点都添加了一个随机方向的向量,而不是采用随机赋值
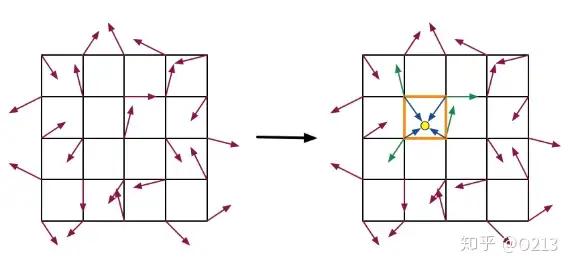
对于晶格内的点,我们需要先生成四个顶点指向该点的向量(如上图),然后利用生成出来的向量与该晶格点上的向量点乘,比如左下角的点为P0,$\vec{P}$为执行晶格内点的向量,$\vec{P0}$为该晶格点随机生成的向量,那么结果就是
$dot(p,p0)$,在得到了结果以后在跟ValueNoise一样,先X轴插值,再Y轴插值
float PerlinNoise(float2 p){
float2 pi = floor(p);
float2 pf = frac(p);
float2 w = pf * pf * pf*(6 * pf * pf - 15 * pf +10);
float v1 = lerp(
dot(hash22(pi + float2(0.0,0.0)),pf -float2(0.0,0.0)),
dot(hash22(pi + float2(1.0,0.0)),pf -float2(1.0,0.0)),w.x);
float v2 = lerp(
dot(hash22(pi + float2(0.0,1.0)),pf -float2(0.0,1.0)),
dot(hash22(pi + float2(1.0,1.0)),pf -float2(1.0,1.0)),w.x);
return lerp(v1,v2,w.y);
}
WorleyNoise
又被称之为泰勒多边形,细胞噪声。可以用于体积云的制作等方面。而一个WorleyNoise噪声的生成也与我们前面两个的生成不太一样。这一次我们不再是基于晶格来生成,而是基于晶胞(虽然文章是这么说的,但是我看了下实现还是靠晶格来实现的)。
一个细胞噪声的生成大致如下,
1.我们先划分好晶格,然后确定输入点所在的晶格
2.确保自己所在的晶格以及周围八个晶格,共九个晶格内一定最少有一个特征点。
3.求出我们的点到九个晶格内特征点的最短路径。最短路径便是该点的值
WorleyNoise的生成就好比是在一些点上来蔓延开,跟力扣上面的小岛问题很像。我们这里就直接给出代码,代码的来源在参考中可以找到,这里也只是做一个讲解来帮助理解.
float2 random2(float2 p)
{
return frac(sin(float2(dot(p, float2(127.1, 311.7)), dot(p, float2(269.5, 183.3)))) * 43758.5453);
}
float WorleyNoise(float2 p){
float min_dist = 1000;
float2 pi = floor(p);
float2 pf = frac(p);
for(int m=-1;m<=1;m++){
for(int n=-1;n<= 1;n++){
float2 sp = (pi +float2(m,n));
sp += random2(sp);
float dist= distance(p,sp);
min_dist = min(dist,min_dist);
}
}
return min_dist;
}
首先我们声明了距离变量,和坐标的整数部分与小数部分,需要注意的是这里的整数与小数其实是按照我们的晶格而言的。比如我在第二个晶格内,那这里的整数部分就应该是(1,0)。后面一个循环则是让我们在外面的晶格中生成特定值。我们在固定的点加上一个随机的变量,也就是 **sp+random(sp)**;便是特定值的坐标,由于我们的晶格点是一个正方形的左下角,所以这个做法一定可以在九个晶格内生成一个特定值。
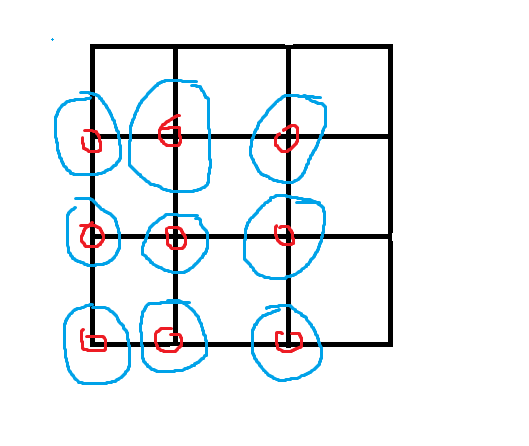
(图画的不好,请勿介意)就如上图,红色的是我们的晶格点。而蓝色所包裹住的晶格则是我们特定值所生成的可能位置,由图很明显就能看出来一定最少能生成四个点在我们的九个晶格内。然后就是循环判断我们的输入点到这几个特征点的距离,并找出最小距离返回。
最终结果展示

分行噪声(FBM)
我们学会了前面的知识点便可以自己去实现一些噪声图,但是这样生成的噪声图十分的无趣,我们可以利用噪声图组合来得到不同的结果。比如将ValueNoise与PerlinNoise相加,这里我们介绍一种让图变得细腻的方法。利用不同的公式,我们便可以得到不同的噪声图,这便是分形噪声。
而分形噪声的实现也很简单,我们只需要讲两张图根据他们的权重加起来即可(没错就是这么粗暴),那么是如何评价一个噪声图的频率是否高呢?
很简单,看他过渡是否多即可。因此白噪声是频率很高的噪音图,那么对于我们的代码应该怎么理解呢。先看以下代码
float ValueNoise(float2 p)
{
float2 pi = floor(p);
float2 pf = frac(p);
float2 w = pf * pf * pf*(6 * pf * pf - 15 * pf +10);
float v1 = lerp(hash21(pi+float2(0.0,0.0)),hash21(pi+float2(1.0,0.0)),w.x);
float v2 = lerp(hash21(pi+float2(0.0,1.0)),hash21(pi+float2(1.0,1.0)),w.x);
return lerp(v1,v2,w.y);
}
float r =ValueNoise(id.xy / scale);
在上文中我们了解到了,scale即是我们一个晶格的长度,即意味着scale越小,我们的参数P越大,这也就意味着我们会生成更多的随机值,生成的贴图过渡也就更加不明显。
这时我们会称这张图的频率很高。那么意味着函数ValueNoise的参数越大,噪声的频率越大。在冯乐乐的博客中给出了一种细腻噪声的方法,
float ValueSum(float2 p){
float f = 0;
p = 4*p;
f += state > 0? abs(ValueNoise(p)) : ValueNoise(p);
p = 2*p;
f+= 0.5 * (state > 0? abs(ValueNoise(p)) : ValueNoise(p));
p = 2*p;
f+= 0.25 * (state > 0? abs(ValueNoise(p)) : ValueNoise(p));
p =2*p;
f+= 0.125 * (state > 0? abs(ValueNoise(p)) : ValueNoise(p));
p = 2 * p;
f+= 0.0625 * (state > 0 ? abs(ValueNoise(p)) : ValueNoise(p));
p = 2*p;
return f;
}
在代码中我们一步步降低了高频噪声的权重。以一个低频的噪声图为基准来将他们相加起来,就可以实现一个以低频噪声图为大概轮廓,高频噪声图来提供细节的噪声图。另外的例子是我们可以通过一张普通的噪声图加上以一个圆为大概轮廓(即圆心的值为1,边上为0,离圆心越远值越小)的噪声图,就可以得到一个随机生成的小岛,具体的可以去给出的参考中红帽子的链接中了解。