前言
最近开了草地渲染觉得很帅。就决定来学习一下如何制作。发现利用到了细分着色器，故此写篇博客来记录一下。
在Unity种我们可以编程的Shader有四个。分别是
- 顶点着色器(Vertex Shader)
- 细分着色器(Tessellation Shader)
- 几何着色器(Geometry Shader)
- 片元着色器(Fragment Shader)
他们在渲染过程中如下
我们今天的主角便是其中的曲面细分着色器(Tessellation Shader) ，曲面细分着色器在我们使用中分为三个步骤。准备数据——生成顶点和边——显示出来。结构如下图
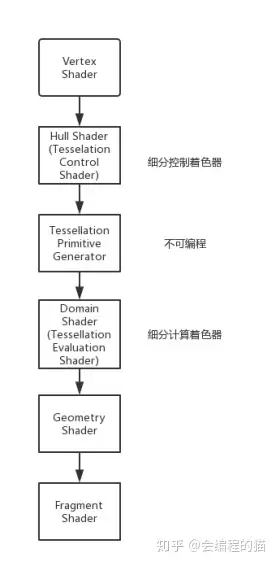
其中的控制着色器便是用于准备数据。而中间的是无法编程也无法配置的，最后一步便是计算结果的细分着色器。
语法结构
在Unity中使用曲面细分着色器第一步需要在Unity中来声明函数和对应的着色器。跟声明顶点着色器和片元着色器一样，语法如下
#pragma hull hullProgram
#pragma domain ds
hull便是我们的细分控制着色器，domain是我们的细分计算着色器。至于具体的内容我们后面再讲。我们现在需要知道细分着色器他的输入是什么，他干了什么事情，他的输出是什么，这样才能更好的去了解该怎么写代码。
Tess输入是一个集合，它包含了每个顶点的属性，其中属性是每个顶点共享的
Tess会根据我们输入的信息，来对面或者是边进行细分。具体的不同的信息需要不同的配置
Tess的输出也很简单，便是我们处理好了的顶点信息。
既然这个Shader需要输入信息，那么就需要写个结构体来存储，代码如下
struct TessVertex{
float4 vertex:INTERNALTESSPOS;
float3 normal:NORMAL;
float4 tangent :TANGENT;
float2 uv :TEXCOORD0;
};
因为我们是细分一个物体，所以只要把原本的顶点信息原封不动的传进来即可，不需要去做什么改动，需要注意的点也就只有vertex的语义本应该是POSITION，现在变成了INTERNALTESSPOS，这是因为编译器会报语义重用的错。
struct OutputPatchConstant{
float edgb[3]:SV_TESSFACTOR;
float inside:SV_INSIDETESSFACTOR;
};
这里还需要声明一个结构体，用于在细分的时候的控制。其中的SV_TESSFACTOR语义是定义了每条边上的细分程度。即指定的边会被分成多少段.而变量数组长度为3是指我们我们的三条边，SV_INSIDETESSFACTOR语义是内部细分度，指定内部再几个维度上被细分。
至此我们便写完了曲面细分着色器的战前准备。接下来我们便要去实现一下他的计算部分。
首先我们需要实现前面指定的曲面细分控制着色器，整个函数如下
[UNITY_domain("tri")] //指输入的图元是三角形
[UNITY_partitioning("fractional_odd")] //拆分edgb的规则
[UNITY_outputtopology("triangle_cw")]//决定了产生的图元的朝向，cw为顺时针，ccw为逆时针
[UNITY_patchconstantfunc("hsconst")]// 指定了计算数值的函数。
[UNITY_outputcontrolpoints(3)] //指hull shader输出的顶点数量
TessVertex hullProgram(InputPatch<TessVertex,3> patch ,uint id:SV_OUTPUTCONTROLPOINTID){
return patch[id];
}
在这个shader中我们大部分的内容都是在配置，而计算的部分较少，前面的几项配置很好理解，参数选择各位可以去网上搜索，这里不再过多叙述，这里要讲的是第四个配置项：**[UNITY_patchconstantfunc(“hsconst”)]**,它指定了一个方法，用于决定怎么计算细分线段。代码如下
OutputPatchConstant hsconst(){
OutputPatchConstant o;
o.edgb[0] = _TessellationUniform;
o.edgb[1] = _TessellationUniform;
o.edgb[2] = _TessellationUniform;
o.inside = _TessellationUniform;
return o;
}
参数**_TessellationUniform一个float类型的变量，用于控制细分程度。其中可选的参数有两个，分别是InputPatch<TessVertex,3> patch** 和 uint patchID：SV_PrimitiveID，前者是一个Patch，参数TessVertex是我们顶点着色器的输出，3是因为一个三角形有3个顶点，我们可以利用这个变量来控制不同的切分因子，从而实现一些LOD的效果。后者是这个patch的唯一ID。
让我们接着往下看，第六个是**UNITY_outputcontrolpoints(3)**。它是指定了我们每个图元输出的控制点的数量，不一定与输入的数量相同？
最后便是我们的函数主题，它返回值是前面定义好了的顶点数据，而他的输入参数则需要细说虽然我也不会，首先是TessVertex，也就是输入的顶点信息，3则是一个patch，前面说了一个patch可以是三角形，四边形，线段，而我们前面又设置为了三角形，一个三角形有3个顶点嘛，所以这里便写3，而后一个参数uint id:SV_OUTPUTCONTROLPOINTID则是告知我们当前执行的顶点是patch的哪一个，因为该函数一次仅应输出一个顶点。Patch中的每个顶点都会调用一次它。在这里我们也可以写第三个参数 uint patchID：SV_PrimitiveID从而获得patch的id。
接下来我们来实现细分计算着色器的内容
[UNITY_domain("tri")]
VertexOutput ds(OutputPatchConstant trssFactors,const OutputPatch<TessVertex,3> patch,float3 bary:SV_DOMAINLOCATION){
//bary 重心坐标
VertexInput v;
v.vertex = patch[0].vertex * bary.x + patch[1].vertex * bary.y + patch[2].vertex*bary.z;
v.tangent = patch[0].tangent * bary.x + patch[1].tangent *bary.y + patch[2].tangent *bary.z;
v.normal = patch[0].normal *bary.x + patch[1].normal *bary.y + patch[2].normal * bary.z;
v.uv = patch[0].uv*bary.x + patch[1].uv*bary.y + patch[2].uv*bary.z;
VertexOutput o = vert (v);
return o;
}
首先是第一行设置图元类型，不讲了，然后函数的主题，里面包含了顶点信息。输入的参数有细分参数trssFactors（就前面算过的那个）。第二个是patch不多说了，第三个参数bary则是重心空间（以重心为原点的坐标系）下的系数。用该系数与重心坐标还原到模型空间，相关的信息可以去看初中数学关于重心的解释。总之我们可以通过系数来获得一个顶点在原始三角形的相对位置。
最后我们将所有的顶点都转化到投影空间，vert函数如下
VertexOutput vert(VertexInput i){
VertexOutput o;
o.vertex = UnityObjectToClipPos(i.vertex);
o.uv = i.uv;
o.normal =i.normal;
o.tangent = i.tangent;
return o;
}
最终效果如下，完整代码可以再参考资料第二个中找到
总结：我们首先是在曲面计算着色器中来配置相关的信息。通过输入的原始面片，我们可以计算出在这个面片内所细分出来的顶点的重心坐标，然后在细分着色器中来具体的计算出它的值。曲面细分着色器现在常用于处理LOD，原理则是在不同的情况下选择不同的细分因子，具体可以从Unity的官方例子中和参考资料中找到。
曲面细分参考
几何着色器介绍
如果说曲面细分着色器是在已有的基础上依靠规则增加顶点，那我们的几何着色器就是无中生有，在已有的定点上来生成新的顶点，而且可以生成不止一个，十分的厉害。
现在让我们来看看一个最简单的几何着色器长什么样
#pragma geometry geom
[maxvertexcount(4)]
void geom(point v2g input[1],inout PointStream<g2f> outStream){
g2f o=(g2f)0;
o.vertex=input[0].vertex;
o.uv=input[0].uv;
outStream.Append(o);
}
第一行定义函数，从第二行才是真正的属于几何着色器部分。他定义了我们单次调用的最大可以生成多少个顶点，我们在后面的具体代码中添加到流中的顶点数量不能超过这个。处于性能考虑，这个最大定点数应该尽可能小。第三行是我们的函数主体，他不需要有返回值，而是直接把返回值写入到流中，也就是PointStream
与前面的类型相同，我们输出流的类型也是分为了点，线，面。他们的类型分别为PointStream,LineStream,TriangleSteam三种。 我们只需要定义好顶点的位置然后输入到流中即可。需要注意的是，几何着色器不会保留原来的信息，所有的输出都要我们自己来重新定义
上面的代码就是将原本模型都只输出成一个点，如下图
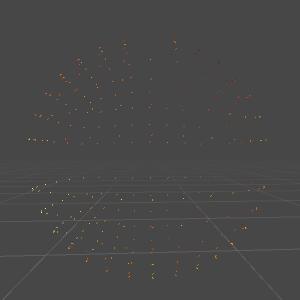
在参考资料中我们可以找到Line版本和Triangle版本。
几何着色器作用
因为几何着色器具有更改显示的原理，因此我们可以利用其来做一些特效，比如一些消散效果，就是通过判断点的坐标值来选择性的将他们变成点或者是面，从而达到了一种自然的消散效果。
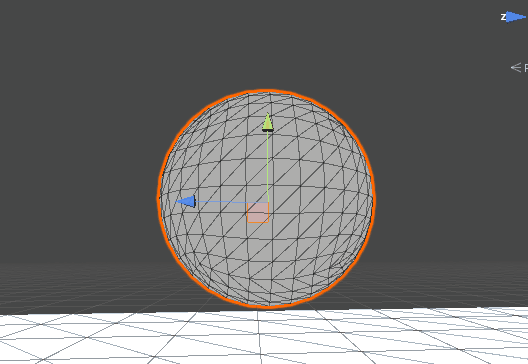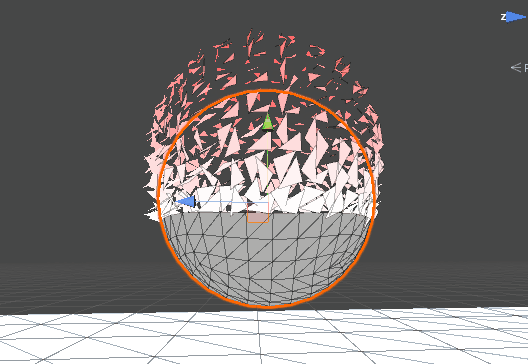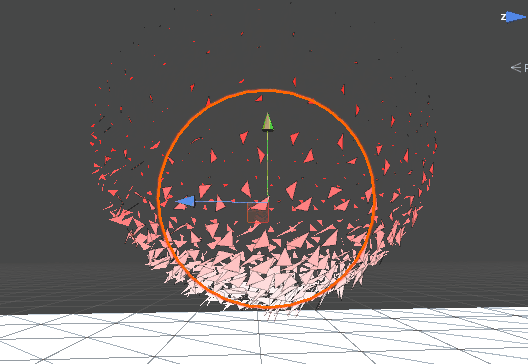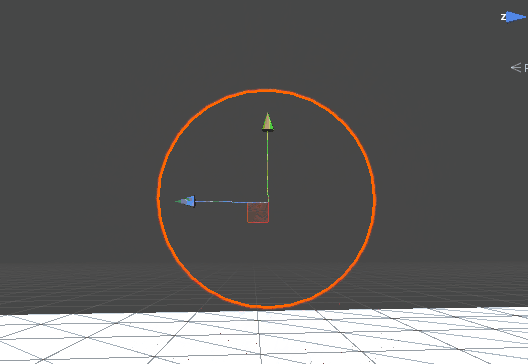其他人的效果图
也可以通过一些相关的信息，比如顶点法线方向，来构建一些我们需要的效果，比如一个会缩放的 “点” 球。这些特效本文也不给出代码了（因为我自己都没写）。
我们也可以通过与曲面细分着色器相结合来生成GPU版本的草地，虽然据说效率不如其他的办法，且适用性比较低（在手机端几何着色器不常用）。但是可定制化十分的高。我们也是通过这个例子来具体讲解几何着色器的使用，代码中关于一些结构体的传递，里面都基本上都说只有uv和vertex数据，因此就不放出来了，只放关键代码
[maxvertexcount(3)]
void geom(point t2g input[1],inout TriangleStream<t2g> outstream){
float3 pos = input[0].vertex;
float3x3 facingRotationMatrix = AngleAxis3X3(rand(pos) * UNITY_TWO_PI,float3(0,1,0));
float3x3 bendRotationMatrix = AngleAxis3X3(rand(pos.zzx) * _BendRotationRandom* UNITY_PI * 0.5f,float3(0,0.2,0.5));
float3x3 transform = mul(facingRotationMatrix,bendRotationMatrix);
float height = (rand(pos.zyx) * 2 - 1) * _BladeHeightRandom + _BladeHeight;
float width = (rand(pos.xzy) * 2 - 1) * _BladeWidthRandom + _BladeWidth;
outstream.Append(vertexOutput(pos + mul(transform,float3(width,0,0)),float2(0.0,0.0)));
outstream.Append(vertexOutput(pos + mul(transform,float3(-width,0,0)),float2(1.0,0.0)));
outstream.Append(vertexOutput(pos + mul(transform,float3(0,height,0)),float2(0.5,1.0)));
}
关于AngleAxis3x3，他随机返回一个旋转矩阵用于控制草的弯曲和旋转。其中我们的代码中facingRotationMatrix负责草的旋转，而bendRotationMatrix负责草的弯曲，
后面的代码中我们在面片的第一个顶点上生成了一个三角形，并重新赋予了uv值，达到让每个草的uv独立，而不是整个草地用一套uv值。
然后便是添加流中，这里的添加顺序也要注意，只有顺时针的时候才能被正常显示出来，而我在关闭了剔除，所以这里的顺序不用关心。
一个草地的核心代码也就是如此的简单，我们利用曲面细分来生成更多的顶点，然后用几何着色器在顶点上生成一个三角形。至于代码的融合就交给各位读者来自己尝试一下了。最终生成的草地效果如下
我们的草地还有许多的不足，比如没有与物体的交互，无法接收阴影，弯曲效果太差，没有随风摇晃的效果（等我实现了我会回来补充）。这些效果仍然需要我去慢慢的学习，学习永无止境，我们不能因为短时间没有效果便选择放弃。愿，在以后的学习之路我们可以越走越远。