游戏Ai知识汇总

一个HTN大致是由整个AI的核心作用域（domain）,存储AI数据的数据库（worldState），感知器（sensors）,计划组织者（planner），执行者（plan Runner）组成，Plan的单位为Task。而一个HTN的基本流程为先由开发者设定好相关的AI行为，在运行时AI会根据先决条件与对worldState的影响最终得到一条可以执行的行为链，
再由我们的PlanRunner来执行

domain，WorldState

domain便是我们的整个AI的核心，又或者可以理解为是Task的存储中心。它包含了一个HTN的全部组成，比如worldState等。而worldState则是我们AI对信息的一个存储地。感觉与行为树中的黑板没有区别

Task

task是HTN的核心，task主要分为了两种compound task(复合任务)与primitive task(原子任务)，除此之外还有一种特殊类型Method(方法),primitiveTask是我们最底层的任务，他主要是由conditions(条件),operator(行为),effect(影响) 组成，primitiveTask是我们的Plan的组成主题，他是我们的执行主体，一串的primitiveTask则是一个解决方案，我们称之为Method，而CompoundTask则是包含了一系列的method，即拥有多种解决方式，这样看下来就很明了了，primitiveTask是最基础的行为，method则是一种解决办法，而compoundTask是一个目标，compoundTask包含了Method，而method则又包含了compoundTask和primitiveTask（这里是因为我们在某个解决方案下又有目标可以选，比如我们想要治疗自己，治疗自己是一个目标。即是一个compound，他可以选择从背包里面拿出药剂来使用（前提是有），也可以自己坐在地上养伤，这两个分支便是两个method，在使用药剂的method下，我们又有两个分支可以解决，分别是自己合成一个和自己去买一个，这便是两个分支，也就是多出来了两个目标，因为目标是由选择构成的，我们不能说选择下继续选择，而是在为了达到这个目标，我们先去完成他的前置目标，）。compoundtask仅仅是一个method的容器，它代表了某个目标的多个选择集合。算是对分支的封装

一个HTN的最终组成便应该是CompoundTask->method->taskbase(可以为compoundTask或primitiveTask).

Planner 与 PlanRunner

我们角色的每一个行为与目标设置好了以后保存在Domain中。但在执行中我们是会根据目标的优先级来获得一条primitiveTask的列表，他表示我们真正要执行的行为，而从Domain中找到这条列表的过程便是Plan，找出这条Plan的过程中并不会执行，而是在找完以后确定了下来才交给物体真正的执行，这个执行便是PlanRunner。

Finding a Plan ：我们会根据目标的优先级，想一颗树一样递归下来，并最终获得某个Method下的顺序primitiveTask组合。在规划的过程中我们会获得一份WorldState的副本，然后在副本上更改模拟任务的执行，看是否可以达到完成的目的。从根开始，他会去compoundTask中从上往下找可行的Method，进入method后，开始从上往下执行primitiveTask，并通过判断WorldState与添加effect来达到模拟的目的。如果该Method是可行的，那么Planner便会退出，并返回一个primitiveTask的列表交给PlanRunner执行。在普通的情况下我们是通过自己手动来调整优先级的方式来获得一个计划，不考虑使用启发式算法来控制计划的生成

为了找到更好的计划来应对突发状况，我认为可以采用下面的办法：

将所有可行的计划排列，当当前的计划无法执行的时候我们会会根据优先级来获得下一个可行的计划，在上面的参考文章中称之为方法遍历记录（MTR），需要明确的是我们的最上层的目标还是同一个，比如攻击敌人的行为中，我们或许可以有丢石头攻击和拿树干攻击敌人，他们之间的前提便是与敌人的距离，当与敌人的距离在近战攻击范围内时，我们便会近战攻击（优先级最高），当在近战攻击范围外远程攻击范围内的时候我们就会丢石头（优先级中间），最后便是跑向敌人。

如果我们采用了优先级选择的方式来快速更改计划，那需要注意每个物体的条件，他可能会跳过某些method，这时候最好是通过worldState来保证顺序，而不是去修改Method或者primitiveTask。

在某些情况下我们可能会需要并行执行某些任务，这可以通过更改primitiveTask的行为来做到，但是破坏了封装性，解决办法有很多，比如primitiveTask封装一个行为树，或者是创立两个domain。让他们通过WorldState来决定，比如下半身的domain负责寻路，如果他确定了目标会将worldState某个状态改为True，然后上半身的domain以此为判断来判断相关决策。

优化相关

HTN的主要消耗在于Plan 的过程，因此减少Plan是我们的优化的一个大方向，最基础的方式有

削弱task的Condition，这样可以让我们在执行计划的时候对环境有更大的包容性，不至于因为一小点的变化就去重新计划。
如果WorldState的状态没有变化，我们可以继续执行上一次得到的Plan，这样也不用重新计划了，
对CompoundTask 与Method 也加上Condition，这样可以达到剪枝的目的。
局部计划：即Planner不完全分解出来一个完整的计划，我们只计划几个步骤。这可以适用于情况多变的局势，因为未来的计划执行的概率不大，因此我们不用计划太远。比如我们的敌人是在我们的攻击范围之外，那AI会先寻路过去再攻击他，寻路过去是个漫长的过程，再路上可能会发生变故，因此它后面的攻击敌人不一定是一定会执行到的（这里只是举例，后续可能会有很多的method，重新去遍历他们会浪费时间）。因此我们可以将寻路与攻击分开。下面的代码是旧计划

Compound Task [BeTrunkThumper]
    Method [WsCanSeeEnemy == true]
        Subtasks [NavigateToEnemy(), DoTrunkSlam()]

Primitive Task [DoTrunkSlam]
Operator [DoTrunkSlamOperator]
Compound Task [NavigateToEnemy]
Method […]
 Subtasks […]

变成了下面这样，因此我们只计划了寻路，寻路后面的我们可以暂时不关心，只用通过WorldState来将他们给隔离开即可。从而达到了局部计划的目的

Compound Task [BeTrunkThumper]
    Method [WsCanSeeEnemy == true, WsEnemyRange > MeleeRange]
        Subtasks [NavigateToEnemy()]
    Method [WsCanSeeEnemy == true]
        Subtasks [DoTrunkSlam()]
Primitive Task [DoTrunkSlam]
Operator [DoTrunkSlamOperator]
Compound Task [NavigateToEnemy]
Method […]
 Subtasks […]

总之，对HTN的优化大部分在于对Plan的优化，我们可以通过减少遍历次数来获得优化效果

GOAP

一个GOAP的简单框架，该例子中的搜索组合用的还是正向搜索，不太完美符合GOAP的原始定义，不过想要改成反向搜索也很简单。可以自己看需求修改
GDC生肉版本分享

极度恐慌GOAP的技术分享

烟雨文章

寻路

A*寻路的优化

避障

转向行为(SteeringBehavior)

视频介绍+代码

一篇熟肉文章

VO避障

RVO避障

ORCA避障

避障算法ORCA整理–精简版

流场寻路(Flow Field Pathfinding)

流场寻路简介

简易的流场寻路框架

Ai的判断

模糊逻辑（Fuzzy Logic）

什么是逻辑模糊

在现实生活中，会有许多的事物是无法用一个确定的值来描述的，比如成绩的是否优秀，不能简单的定下一个值来说：高于90分的才是优秀，那89分的就很不服，因为89和90的差距并不大。模糊逻辑便可以帮助我们解决这个问题，让我们在计算机中实现类似于人的思考，

在游戏中以各种方式使用模糊逻辑。例如，可以使用模糊逻辑来控制机器人或其他npc。也可以使用它来评估玩家构成的威胁。
我们可以通过模糊逻辑来对敌人的防御，血量，伤害等数据来给出一个数值，用于行为树或者是FSM中用于控制AI的行为。

如果使用逻辑模糊

一个逻辑模糊的流程如下图

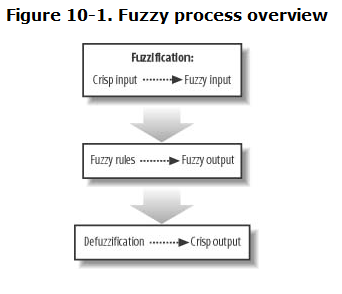
第一步被称之为模糊化过程，在这一步中我们将清晰明了的数据给转化为模糊数据。比如给定一个人的体重，我们可以给出这个人体重不足，理想体重，超重的所在程度。然后我们根据所得到的结果来去匹配自己的规则。比如我们提前制定好了以下规则

1.如果超重且不活跃，则经常锻炼

2.如果超重且活跃，则适度饮食

我们将体重与活跃程度得到的模糊输入给结合起来，就可以产生一个符合规则的模糊输出。但一个模糊化的输出对于我们而言是没有太大作用的，无法通过一个模糊输出来更改AI的决策，因此还需要将模糊化输出给量化，变成一个确定清晰的值，这一步被称之为 去模糊化

模糊化

对于模糊化操作需要一个模糊函数（也称之为特征函数）。如下图

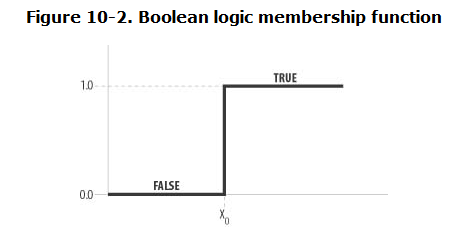
我们对输入的清晰值与X0进行比较，如果大于X0就返回true，反之则返回false，回到体重的例子，我们无法定义一个确定的区间来说明那个阶段是肥胖哪个阶段是瘦弱。因此我们可以采用一个过渡来解决这个问题，如下图

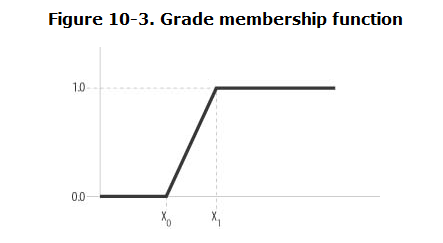
在x0与x1之间我们添加了一个过渡，我们可以成为肥胖占比，那么现在我们就可以说你在X0之前是瘦子，X1之后是肥胖。越靠近X1就越胖。回到重量的例子，假设这个函数代表超重的成员。设x0等于175，x1等于195。如果一个人体重170磅，那么他的肥胖比例为0，也就是说，他不超重。如果他体重185磅，那么他肥胖比例为0.5——他有点超重。

一般来说我们感兴趣的输入变量他不只属于一个集合，换到重量的例子中来说，他不只有肥胖比例，他或许还可以拥有瘦弱比例，（瘦弱的特征函数的输入也是重量），如下图

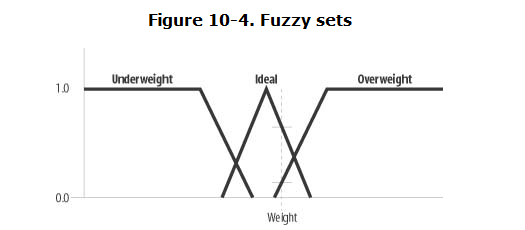
一般来说应该多尝试一些模糊集（即一个函数端），也有建议说使用七个模糊集来充分定义。如下图

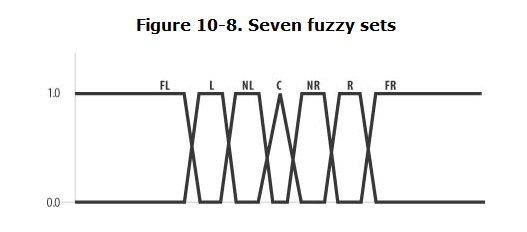
七个模糊集分别为中心、近右、右、远右、近左、左和远左。根据您的问题，这些类别可以是任何类型。例如，为了表示角色扮演游戏中玩家和非玩家角色的对齐，您可能有模糊集，如中性、中性善、善、混乱善、中性恶、恶和混乱恶。

经验说每个集合应该与其邻居重叠大约25%。特征函数可以是我们任意形状的函数，由具体的类型来决定。

Hedges（不知道中文）

用于修改返回的成员函数的结果。我们完全可以不用这东西，但是论文中可能会有，这里提一嘴

模糊规则（Fuzzy Rules）

当我们获得了一些值的隶属度以后，我们便可以以一些规则来组合他们，来获得一些输出。获得的输出也被称之为结果。

一般的逻辑处理符有 AND，OR，NOT，也就是与或非。（当然具体的实现还是得看自己）。
$A AND B = MIN(A,B),A OR B = MAX(A,B),NOT A = 1 - A$

假设你有一个电子游戏，正在使用模糊系统来评估生物是否应该攻击玩家。输入变量包括射程、生物生命值和对手排名。每个成员函数如下图

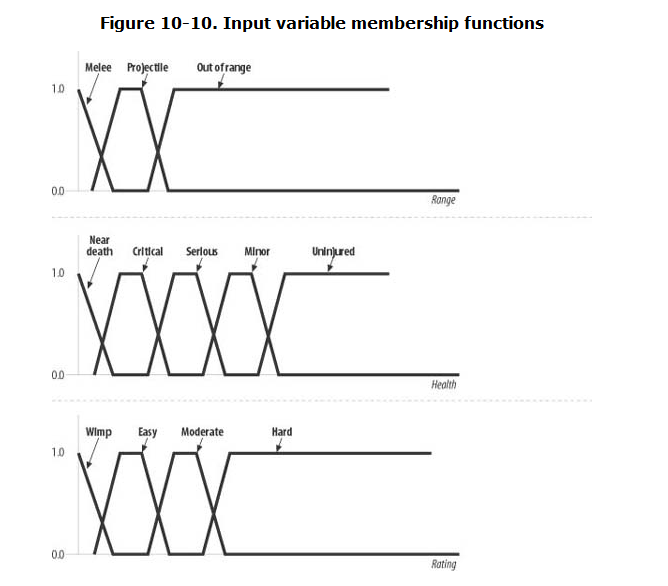
本例中的输出动作可以是逃跑、攻击或什么都不做。我们可以编写一些规则，看起来如下所示：

if(可以近战攻击 AND 没有受伤) AND 打得过
    attack
if(不在攻击范围) AND 没有受伤
    do nothing
if(NOT 超出范围 AND NOT 受伤) AND （NOT 简单）
    flee

需要注意的是上面只是规则，if内的attack也不是一个特定的动作，而是一个值，是我们经过了模糊规则处理过后的返回值，他代表了输出模糊集中的隶属度（the strength of each rule represents the degree of membership in the output fuzzy set.）

经过上面的规则，和我们的输入值我们可以得到以下的结果

attack = 0.2
do nothing = 0.4
flee  = 0.7
//代码实现如下
degreeAttack = MIN(MIN (degreeMelee, degreeUninjured),1.0 - degreeHard);

degreeDoNothing = MIN ( (1.0 - degreeMelee),degreeUninjured);

degreeFlee = MIN (MIN ((1.0 - degreeOutOfRange),(1.0 - degreeUninjured)),(1.0 - degreeWimp));

对于得到的结果，我们可以直接选择最大的可能性（在本例中是逃跑）来执行，也可以自己来处理

我们可以直接利用隶属度来当权重值然后随机判断，也可以反模拟化将其给变成真正的数值，一般来说我们采用了是一个输出函数，我们为每一个行为都赋予以个权重值，比如逃跑的权重值为-10，什么都不做的权重为1，进攻的权重为10，那么我们反模糊得到的结果为
$(0.7)(10) + (0.4)(1) + (0.3)(10)/(0.7+0.4+0.3) = -2.5$
那么我们就会慢慢逃跑。

总之，我们可以通过自己提前定义好的函数，将所得到的模糊结果处理，最终应用到自己的Ai中去

贝叶斯概率

在某些情况下，我们可以能希望AI可以根据已经发生过的概率来推断出下一次发生的概率。比如，有个敌人的AI，我们可以设置一些障碍陷阱来引诱他，我们不希望AI每次都中招或者每次都不中招，我们看i我它可以根据不确定信息来做出决策，这个时候就可以使用我们的贝叶斯规则。

贝叶斯概率的核心是贝叶斯定理，他的表达式如下
$P(A|B) = P(B|A)*P(A) / P(B)$
其中P(B|A)表示的是在事件A发生的情况下，事件B发生的概率，也被称之为后验概率或似然度。意思是相似概率，**P(B)则是B事件发生的总概率，也叫做先验概率，P(A|B)**则是在B发生后A也发生的概率。是我们想要知道的量

举个例子，有一个病他的发病率为1%，某种检测方法有95%的准确率，即如果患有该病的人进行检测，有95%的概率会显示出阳性结果；而如果没有该病的人进行检测，有5%的概率会误判为阳性。

根据贝叶斯公式，我们可以得到：

**P(患有该病|阳性结果) = P(阳性结果|患有该病) * P(患有该病) / P(阳性结果)

其中，P(患有该病|阳性结果) 表示在获得阳性结果的情况下，患有该病的概率；P(阳性结果|患有该病) 表示在患有该病的情况下，获得阳性结果的概率；P(患有该病) 表示患者本来就患有该病的概率；P(阳性结果) 表示获得阳性结果的概率。

那么最终的结果为

P(患有该病|阳性结果) = 0.95 * 0.01 / (0.95 * 0.01 + 0.05 *(1-0.01)) = 0.16

其中的分母是所有为阳性的结果，其中确诊为阳性的结果为（0.95 * 0.01）,而不确诊依然为阳性的结果是（0.05 * 0.99）,所有阳性的结果是他们加起来的概率。

再举一个例子，假设我们可以给宝箱设下一个陷阱，而敌人则会判断这个宝箱自己是否要打开，宝箱是分为了上锁与没有上锁的状态，那么我们的敌人看到一个宝箱而去打开他的概率是多少呢？
利用我们前面的知识，设P(T|L)为宝箱上锁且是陷阱的概率（这里的概率是在敌人视角下的概率，即敌人看到了一个上锁的宝箱认为他是陷阱的概率），P(T)是宝箱是陷阱的概率，P(L)是上锁的概率。P（L|T）是陷阱并且上锁的了概率，那么我们可以得到一个公式

$P(T|L) = P(L|T) * P(T) / P(L)$

假设游戏中的一个NPC有打开100个箱子的经验，在这100个箱子中有37个是陷阱。在是陷阱的37个箱子中，29个被锁住了。在63个不是陷阱的箱子
中，有18个被锁住了。

那么P(L|T) = 29 / 37 = 0.78

P(T) = 37 / 100 = 0.37

P(L) = P(L|T) * P(T) + P(L|~~T) * P(~~T) = 0.78 * 0.37 + (18/63 = 0.29) * (0.63) = 0.47

最终的结果是 0.78 * 0.37 / 0.47 = 0.61
意味着我们NPC有61%的概率认为这个上锁的箱子是一个陷阱。

那么如果我们的NPC看到了一个没有上锁的箱子，认为他是陷阱的概率为多少呢。

$P(T|~~L) = P(~~L|T) * P(T) / P(~L)$

P(~L|T) = 1 - 0.78 = 0.22

P(T) = 0.37

P(~L) = 1 - P(L) = 0.53

因为开不开锁是一个对立事件，所以可以直接相减。

最终的结果为:0.22 * 0.32 / 0.53 = 0.15

所有我们的NPC认为一个不上锁的箱子是陷阱的概率不大，对于得到的结果怎么应用到我们的实际决策中就可以随意了，可以直接用轮盘赌算法，也可以利用模糊逻辑来让Ai根据自身的状况一起考虑。

贝叶斯网络

有的时候，一个事件的概率不仅仅是一个事情来影响，比如一个宝箱是否上锁会受到是否是个陷阱和是否有宝藏两个事件的影响，而是否是个陷阱又由是否有宝藏影响，画成图来表示如下

那么此时的NPC觉得该打开宝箱的概率是多少呢？
带入贝叶斯公式是

$P(T|L) = P(L|T)P(T)/P(L)$

与上次不同的是我们这里没有给出 P(T)的具体值，因为是否是个陷阱的概率受到了是否有宝藏的影响，所以计算如下

P(T) = P(T|Tr)P(Tr) + P(T|~~Tr)P(~~Tr),

同理P(L)如下

P(L) = P(L|T)P(T) + P(L|~~T)P(~~T)。关于P(L|T)与P(L|~T)则可以通过已知的事件来获得，在这个例子中，宝箱是否上锁的概率不再是只由是否是陷阱来决定，还会因为是否有宝藏而决定(从P(T)的参数可以看出)，

那么NPC认为其中有宝藏的概率是多少呢。

$P(Tr|L) = P(L|Tr) * P(Tr) / P(L)$

其中的P(L|Tr) = P(L|T)*P(T|Tr) + P(L|~~T) * P(~~T|Tr)

举个例子
游戏中的某个NPC有打开100个箱子的经验，其中50个箱子里有宝藏。在这50个宝箱中，有40个宝箱有陷阱，在这40个有陷阱的箱子中，有28个被锁住了。现在，在10个没有陷阱的箱子中，有3个被锁住了。此外，在50个没有宝藏的箱子中，有20个有陷阱。有了这些信息，我们可以计算以下概率：

带入公式：

P(T) = P(T|Tr)P(Tr) + P(T|~~Tr)P(~~Tr) = 0.8 x 0.5 + 0.4 x 0.5 = 0.6

P(L) = P(L|T)P(T) + P(L|~~T)P(~~T) = 0.7 x 0.6 + 0.1 x(1-0.6) = 0.54

P(T|L) = 0.7 x 0,6 / 0.54 = 0.78

而P(Tr) = 0.5 ，P(L) = 0.54,

P(L|Tr) = P(L|T)P(T|Tr) +P(L|~~T)P(~~T|Tr) = (0.7 x 0.8 + 0.3 x 0.2) = 0.62

P(Tr|L) = (0.62 x 0.5) / 0.54 = 0.57

综上所述，我们可以可以发现面对一个箱子，NPC认为是个陷阱的概率变成了了78%，而认为有宝藏的概率变成了54%，

贝叶斯网络的节点越多，运算的数量就会越多，因此再没必要的情况下，不要整太多的节点。

多人Ai

待补充

感知

待补充

深度学习

待补充

遗传算法

待补充

其他网站

AI分享站
 知乎收藏的一些文章

决策层
有限状态机
分层状态机
行为树
寻路
避障
Ai的判断
多人Ai
感知
深度学习
遗传算法
其他网站